Filters
Question type
Study Flashcards

If a population proportion is 0.8 and a sample of size n = 100 is randomly selected from this population, what is the standard deviation of the proportion If a population proportion is 0.8 and a sample of size n = 100 is randomly selected from this population, what is the standard deviation of the proportion ? A) 0.0258 B) 0.0355 C) 0.0400 D) 0.0538 ?


A) 0.0258
B) 0.0355
C) 0.0400
D) 0.0538

E) A) and B)
F) B) and C)

Correct Answer

verifed

verified

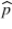If n ≥ 30, we know that the sampling distribution of If n ≥ 30, we know that the sampling distribution of is: A) approximately normal. B) exactly normal. C) suitable for estimating the unknown parameter p. D) unknown, because n ≥ 30 alone tells us nothing substantial concerning the sampling distribution of . is:


A) approximately normal.
B) exactly normal.
C) suitable for estimating the unknown parameter p.
D) unknown, because n ≥ 30 alone tells us nothing substantial concerning the sampling distribution of If n ≥ 30, we know that the sampling distribution of is: A) approximately normal. B) exactly normal. C) suitable for estimating the unknown parameter p. D) unknown, because n ≥ 30 alone tells us nothing substantial concerning the sampling distribution of . .

E) A) and C)
F) None of the above

Correct Answer

verifed

verified

The survival times of adult mosquitoes exposed to a commonly used synthetic pesticide (Phenothrin) follow a gamma distribution, with a mean time until extermination of 48 sec and a standard deviation of 15.18 sec.What is the probability that a random sample of 40 mosquitoes will have an average survival time between 47.5 sec and 48 sec?


A) 0.0832
B) 0.4207
C) 0.4880
D) 0.0120

E) All of the above
F) A) and C)

Correct Answer

verifed

verified

An industrial fan is designed to move 2500 ft3of air per minute, on average.Under normal operating conditions, the standard deviation of air volume moved by this fan is 300 ft3/min.If the fan is operating as designed, what is the probability that the average of 30 randomly selected measurements of fan capacity will be less than 2000 ft3/min?


A) 0.0475
B) 0.0000
C) 0.9525
D) 0.913

E) B) and C)
F) A) and D)

Correct Answer

verifed

verified

Suppose 45% of voters favor candidate A.We can be 67% sure that out of 200 randomly selected voters, at least how many will favor candidate A?


A) 90
B) 87
C) 134
D) 93

E) B) and D)
F) B) and C)

Correct Answer

verifed

verified

B

A population of sports teams consists of 26 individual teams.We wish to randomly sample 4 teams for observation.If each team has an equal likelihood of being selected, what is the probability that any given sample of size 4 will be selected?


A) 1/14,950
B) 4/14,950
C) 1/358,800
D) 4/358,800

E) A) and C)
F) B) and C)

Correct Answer

verifed

verified

If the sample size (n) is large (say, n ≥ 30) , then it is safe to model the sampling distribution of If the sample size (n) is large (say, n ≥ 30) , then it is safe to model the sampling distribution of 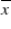as a: A) discrete distribution. B) continuous distribution. C) log-normal distribution. D) normal distribution. as a:


A) discrete distribution.
B) continuous distribution.
C) log-normal distribution.
D) normal distribution.

E) B) and C)
F) A) and B)

Correct Answer

verifed

verified

D

If a population has a variance of 64 and we take a simple random sample of size 25, what will the standard deviation of the sampling distribution of If a population has a variance of 64 and we take a simple random sample of size 25, what will the standard deviation of the sampling distribution of 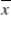be, assuming the Central Limit Theorem holds in this case? A) 0.32 B) 0.625 C) 1.60 D) 3.125 be, assuming the Central Limit Theorem holds in this case?


A) 0.32
B) 0.625
C) 1.60
D) 3.125

E) B) and D)
F) A) and D)

Correct Answer

verifed

verified

The problems associated with sampling without replacement in the simple random sample process are negligible provided:


A) the sample is large relative to the population size.
B) the population is small relative to the sample size.
C) the sample and the population are of roughly the same size.
D) the population is large relative to the sample size.

E) B) and C)
F) None of the above

Correct Answer

verifed

verified

A psychologist randomly samples 28 clinically depressed patients.She subjects each patient to a standardized battery of tests.The average battery test score for the sample is 128.In this example, the number 128 is a:


A) parameter.
B) sampling distribution.
C) statistic.
D) random variable.

E) B) and C)
F) A) and C)

Correct Answer

verifed

verified

Consider a large population with a mean of 150 and a standard deviation of 27.A random sample of size 36 is taken from this population.What is the standard error of the sampling distribution of the sample mean?


A) 4.17
B) 4.50
C) 5.20
D) 5.56

E) A) and D)
F) A) and C)

Correct Answer

verifed

verified

For after-hours emergencies, doctors often use a messaging/paging service to allow patients to contact them.If it is known that 30% of the patients who call the messaging service fail to leave a message for the doctor, what is the probability that out of 80 randomly sampled calls, more than 30 will fail to leave a message?


A) 0.0512
B) 0.9279
C) 0.3750
D) 0.0721

E) B) and C)
F) A) and B)

Correct Answer

verifed

verified

We wish to survey high schools in a particular city.If the city has 22 high schools and we want to select 5 of them, how many unique samples of size 5 are possible?


A) 3,160,080
B) 5,153,632
C) 26,334
D) 2.384 × 1015

E) A) and D)
F) B) and D)

Correct Answer

verifed

verified

In a study whose results were published in the British Medical Journal (Willis et al., 2004) , researchers tested whether dogs can smell cancer in humans.Each dog used in the study was presented with seven urine samples to smell, with only one of the urine samples coming from a patient who had bladder cancer.Taken as a group, the dogs were tested on 54 trials and correctly identified the urine from the cancer patient in 22 trials.If the dogs were just guessing and so had a probability of success p = 1/7, what is the probability they would be correct in 22 or more of the 54 trials?


A) 0.000
B) 0.042
C) 0.087
D) 0.168

E) A) and C)
F) A) and B)

Correct Answer

verifed

verified

The ______________ of a statistic is the probability distribution of the statistic.


A) limiting distribution
B) exponential distribution
C) normal distribution
D) sampling distribution

E) B) and C)
F) None of the above

Correct Answer

verifed

verified

If the standard error of the sampling distribution of a sample proportion is 0.02049 for samples of size 500, then the population proportion must be either:


A) 0.2 or 0.8.
B) 0.3 or 0.7.
C) 0.6 or 0.4.
D) 0.15 or 0.85.

E) None of the above
F) All of the above

Correct Answer

verifed

verified

Let X be the fuel efficiency, in miles per gallon, of a particular vehicle. Suppose X ~ N(μ = 18.5, σ = 2.2) .Find P(18.2 ≤ Let X be the fuel efficiency, in miles per gallon, of a particular vehicle. Suppose X ~ N(μ = 18.5, σ = 2.2) .Find P(18.2 ≤ 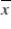≤ 19) if n = 5. A) 0.6950 B) 0.9839 C) 0.1467 D) 0.3129 ≤ 19) if n = 5.


A) 0.6950
B) 0.9839
C) 0.1467
D) 0.3129

E) None of the above
F) B) and C)

Correct Answer

verifed

verified

Which of the following statements about the Central Limit Theorem is true?


A) The Central Limit Theorem states that the sample mean Which of the following statements about the Central Limit Theorem is true? A) The Central Limit Theorem states that the sample mean is always equal to the population mean μ. B) The Central Limit Theorem states that the sampling distribution of the population mean μ is approximately normal provided that n ≥ 30. C) The Central Limit Theorem states that the sampling distribution of the sample mean is approximately normal for large sample sizes (n ≥ 30) . D) The Central Limit Theorem states that the sample mean is equal to the population mean μ provided that n ≥ 30. is always equal to the population mean μ.
B) The Central Limit Theorem states that the sampling distribution of the population mean μ is approximately normal provided that n ≥ 30.
C) The Central Limit Theorem states that the sampling distribution of the sample mean Which of the following statements about the Central Limit Theorem is true? A) The Central Limit Theorem states that the sample mean is always equal to the population mean μ. B) The Central Limit Theorem states that the sampling distribution of the population mean μ is approximately normal provided that n ≥ 30. C) The Central Limit Theorem states that the sampling distribution of the sample mean is approximately normal for large sample sizes (n ≥ 30) . D) The Central Limit Theorem states that the sample mean is equal to the population mean μ provided that n ≥ 30. is approximately normal for large sample sizes (n ≥ 30) .
D) The Central Limit Theorem states that the sample mean Which of the following statements about the Central Limit Theorem is true? A) The Central Limit Theorem states that the sample mean is always equal to the population mean μ. B) The Central Limit Theorem states that the sampling distribution of the population mean μ is approximately normal provided that n ≥ 30. C) The Central Limit Theorem states that the sampling distribution of the sample mean is approximately normal for large sample sizes (n ≥ 30) . D) The Central Limit Theorem states that the sample mean is equal to the population mean μ provided that n ≥ 30. is equal to the population mean μ provided that n ≥ 30.

E) C) and D)
F) A) and D)

Correct Answer

verifed

verified

C

In the natural world, the number of measurable variables that follow a normal distribution is quite remarkable.Many of these measurable variables are actually the sum of other independent variables.The Central Limit Theorem helps explain this phenomenon because:


A) the Central Limit Theorem states that all measurable variables follow a normal distribution.
B) the Central Limit Theorem states that for a sufficiently large number of variables, the sum of these variables will be approximately normally distributed.
C) the Central Limit Theorem states that for large sample sizes, all measurable variables will follow a normal distribution.
D) the Central Limit Theorem states that because nature is normative, variables found in nature will be at least approximately normal.

E) A) and B)
F) A) and D)

Correct Answer

verifed

verified

Consider the following discrete population distribution: ​ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies.


A) μ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 = 5.4, σ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 = 2.069
B) μ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 = 1.08, σ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 = 0.4138
C) μ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 = 5.4, σ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 = 0.9253
D) μ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 = 5.4, σ Consider the following discrete population distribution: ​ ​ We randomly draw samples of size 5 from this population using the simple random sampling technique.If we know that μx = 5.4, σx= 2.069, what are the mean and the standard deviation of the sampling distribution of sample means? Assume the Central Limit Theorem applies. A) μ = 5.4, σ = 2.069 B) μ = 1.08, σ = 0.4138 C) μ = 5.4, σ = 0.9253 D) μ = 5.4, σ = 0.4138 = 0.4138

E) B) and D)
F) A) and B)

Correct Answer

verifed

verified

Showing 1 - 20 of 50

Related Exams

Exam 1

Why Study Statistics

11 Questions

Exam 2

An Introduction to Statistics and Statistical Inference

53 Questions

Exam 3

Tables and Graphs for Summarizing Data

28 Questions

Exam 4

Numerical Summary Measures

34 Questions

Exam 5

Probability

54 Questions

Exam 6

Random Variables and Discrete Probability Distributions

23 Questions

Exam 7

Continuous Probability Distributions

45 Questions

Exam 9

Confidence Intervals Based on a Single Sample

51 Questions

Exam 10

Hypothesis Tests Based on a Single Sample

65 Questions

Exam 11

Confidence Intervals and Hypothesis Tests Based on Two Samples or Treatments

45 Questions

Exam 12

The Analysis of Variance

12 Questions

Exam 13

Correlation and Linear Regression

57 Questions

Exam 14

Categorical Data and Frequency Tables

23 Questions

Exam 15

Nonparametric Statistics

66 Questions

Show Answer