Filters
Question type
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
F) B) and E)
G) A) and E)
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Question 52
Multiple Choice
Find the integral using the indicated substitution. 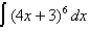 ,
, 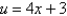
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) None of the above
F) A) and B)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Question 53
Essay
Let ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://d2lvgg3v3hfg70.cloudfront.net/TB5971/11eaa3e5_55a5_f8b3_9f8f_d3756c7e286e_TB5971_11.jpg) .
a.Use Part 1 of the Fundamental Theorem of Calculus to find
.
a.Use Part 1 of the Fundamental Theorem of Calculus to find ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://d2lvgg3v3hfg70.cloudfront.net/TB5971/11eaa3e5_55a6_1fc4_9f8f_139ea51780a1_TB5971_11.jpg) .
b.Use Part 2 of the Fundamental Theorem of Calculus to integrate
.
b.Use Part 2 of the Fundamental Theorem of Calculus to integrate ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://d2lvgg3v3hfg70.cloudfront.net/TB5971/11eaa3e5_55a6_1fc5_9f8f_035219f062fe_TB5971_11.jpg) to obtain an alternative expression for F(x).
c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1
If f is continuous on [a, b], then the function F defined by
to obtain an alternative expression for F(x).
c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1
If f is continuous on [a, b], then the function F defined by ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://d2lvgg3v3hfg70.cloudfront.net/TB5971/11eaa3e5_55a6_46d6_9f8f_4f4da712b2a5_TB5971_11.jpg) is differentiable on (a, b), and
is differentiable on (a, b), and ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://d2lvgg3v3hfg70.cloudfront.net/TB5971/11eaa3e5_55a6_46d7_9f8f_c3bc40309522_TB5971_11.jpg) The Fundamental Theorem of Calculus, Part 2
If f is continuous on [a, b], then
The Fundamental Theorem of Calculus, Part 2
If f is continuous on [a, b], then ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://d2lvgg3v3hfg70.cloudfront.net/TB5971/11eaa3e5_55a6_46d8_9f8f_91f5f7a42169_TB5971_11.jpg) where F is any antiderivative of f, that is,
where F is any antiderivative of f, that is, ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://d2lvgg3v3hfg70.cloudfront.net/TB5971/11eaa3e5_55a6_6de9_9f8f_cf10a69dd2cf_TB5971_11.jpg) .
.
Correct Answer

verified
Correct Answer
verified
Question 54
Multiple Choice
The given expression is the limit of a Riemann sum of a function f on [a, b]. Write this expression as a definite integral on [a, b]. ![The given expression is the limit of a Riemann sum of a function f on [a, b]. Write this expression as a definite integral on [a, b]. A) B) C) D)](https://d2lvgg3v3hfg70.cloudfront.net/TB5971/11eaa3e5_55a7_f49f_9f8f_57d42db5275a_TB5971_11.jpg)
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) A) and C)
F) All of the above
F) All of the above
Correct Answer

verified
Correct Answer
verified
Question 55
Multiple Choice
The velocity function (in meters per second) is given for a particle moving along a line. Find the distance traveled by the particle during the given time interval. 
A) 100 m
B) 72 m
C) 36 m
D) 64 m
E) 68 m
F) A) and E)
G) A) and D)
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Question 56
Essay
Find the indefinite integral. 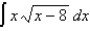
Correct Answer

verified
Correct Answer
verified
Question 57
Multiple Choice
Determine a region whose area is equal to  .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
F) B) and D)
G) C) and D)
G) C) and D)
Correct Answer

verified
Correct Answer
verified
Question 58
Multiple Choice
Evaluate the integral. 
A) 1.000
B) -0.500
C) 0.250
D) -1.000
E) ![]()
F) A) and D)
G) A) and C)
G) A) and C)
Correct Answer

verified
Correct Answer
verified
Question 59
Multiple Choice
Evaluate the integral. 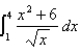
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
F) C) and D)
G) A) and C)
G) A) and C)
Correct Answer

verified
Correct Answer
verified
Question 60
Multiple Choice
Evaluate the indefinite integral. 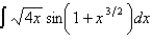
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
![]()
F) B) and C)
G) A) and E)
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Question 61
Essay
Evaluate the indefinite integral. 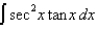
Correct Answer

verified
Correct Answer
verified
Question 62
Short Answer
The table gives the values of a function obtained from an experiment. Use the values to estimate  using three equal subintervals with left endpoints.
w
0
1
2
3
4
5
6
f (w)
9.7
9.1
7.7
6.1
4.2
-6.6
-10.3
using three equal subintervals with left endpoints.
w
0
1
2
3
4
5
6
f (w)
9.7
9.1
7.7
6.1
4.2
-6.6
-10.3
Correct Answer

verified
Correct Answer
verified
Question 63
Essay
Find a function f (x) such that 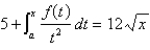 for
for  and some number
a.
and some number
a.
Correct Answer

verified
Correct Answer
verified
Question 64
Essay
Evaluate by interpreting it in terms of areas. 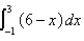
Correct Answer

verified
Correct Answer
verified
Question 65
Essay
Use the Midpoint Rule with 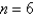 to approximate the integral. Round the answer to 3 decimal places.
to approximate the integral. Round the answer to 3 decimal places. 
Correct Answer

verified
Correct Answer
verified
Showing 81 - 95 of 95
Related Exams